//iklan otomatis

GoJo pepPo

"ikatlah ilmu dengan menulisnya" salam,Gojo peppo

Showing posts with label otomata. Show all posts
Showing posts with label otomata. Show all posts

Sunday, 23 March 2014

Software Simulator Otomata

Software Simulator Otomata

March 23, 2014 otomata , 0 Comments
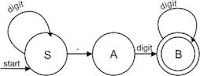
Di artikel sebelumnya (Pengenalan Teori Otomata) kita udah tau apa itu otomata, dan untuk cara memodelkannya kalian bisa baca di Finite State Automata (FSA).
Nah di artikel ini saya akan berbagi dengan kalian tentang aplikasi untuk memodelkan otomata secara otomatis, jadi kagak bingung untuk nyari hasilnya :D

Sebelum kalian menggunakan aplikasi ini, pastikan di komputer harus terinstall java dulu, karna aplikasi ini lahir dari keluarga java.
  1. JFLAP
    JFlap Software Simulator Otomata 
    JFLAP adalah paket perangkat grafis yang dapat digunakan sebagai bantuan dalam belajar konsep dasar Bahasa Formal dan Teori Automata. JFLAP dapat digunakan untuk bereksperimen dengan bahasa formal yang termasuk topiknondeterministic finite automata, nondeterministic pushdown automata, multi-tape Turing machines, several types of grammars, parsing, and L-systems. Selain membangun dan menguji contoh-contoh untuk ini, JFLAP memungkinkan seseorang untuk bereksperimen dengan bukti konstruksi dari satu bentuk ke bentuk lainnya, seperti mengubah sebuah NFA ke DFA ke keadaan minimal DFA untuk ekspresi reguler atau tata bahasa reguler.

    Sekarang JFLAP udah Version 7.0 RELEASED August 28, 2009
    Website : http://www.jflap.org/
    Tutorial : http://www.jflap.org/tutorial/
    Download : http://www.cs.duke.edu/csed/jflap/log/form.php
  2.  jFAST  a Java Finite Automata Simulator
    jFast Software Simulator Otomata
    jFAST adalah silmulator sederhana, alat yang mudah digunakan untuk membuat, mengedit, dan simulasi finite automata dan state machines. jFAST menyediakan metode yang sederhana dan intuitif berinteraksi dengan berbagai jenis didukung finite state machines (FSM), termasuk deterministic finite automata (DFA), non-deterministic finite automata (NFA), pushdown automata (PDA), state machines (SM), dan Turing machines (TM). jFAST juga menyediakan untuk pengguna dengan kemampuan untuk memeriksa FSM mereka pada input yang berbeda, dan memberikan pesan yang jelas dan bermakna ketika kesalahan ditemui.

    Sekarang jFAST udah Version 1.2 RELEASED May 26, 2006
    Website :     http://jfast-fsm-sim.sourceforge.net/
    Tutorial : http://jfast-fsm-sim.sourceforge.net/
    Download :     http://sourceforge.net/projects/jfast-fsm-sim/
  3. Visual Automata Simulator
    Visual Automata Simulator

    Sebuah alat     untuk simulasi, visualisasi dan mengubah finite state automata dan Turing Machines    .
    Aplikasi kecil ini memungkinkan untuk membuat dan mensimulasikan setiap deterministik atau Non-Deterministic Finite Automata (DFA atau NFA) serta Mesin Turing (TM).
    Telah terinspirasi oleh kelas CS411 (Automata Theory) yang diajarkan oleh Prof Galles dan CS601 (Object-Oriented Software Development) yang diajarkan oleh Prof Parr.
    Ditulis seluruhnya di Java (menggunakan Swing untuk GUI)

    Sekarang VAS udah Version 1.2.2 RELEASED November 24, 2006
    Website :     http://www.cs.usfca.edu/~jbovet/vas.html
    Download :     http://www.cs.usfca.edu/~jbovet/vas/download/generic.zip
>>>Tulisan ini bisa kalian download dalam bentuk PDF Download Software Simulator Otomata - Gojo peppo.pdfdisini
By di No comments:
Label:

Friday, 11 November 2011

Finite State Automata (fsa)

November 11, 2011 otomata , 2 Comments
  • Model matematika yang dapat menerima input dan mengeluarkan output
  • Memiliki state yang berhingga banyaknya dan dapat berpindah dari satu state ke state lainnya berdasar input dan fungsi transisi
  • Tidak memiliki tempat penyimpanan/memory, hanya bisa mengingat state terkini.
  • Mekanisme kerja dapat diaplikasikan pada : elevator, text editor, analisa leksikal, pencek parity.
0
1
0
1
1
0
1

FA

Contoh pencek parity ganjil :
pencekganjil

Misal input : 1101
         Genap 1 Ganjil 1 Genap 0 Genap 1 Ganjil
         diterima mesin
Misal input : 1100
         Genap 1 Ganjil 1 Genap 0 Genap 0 Genap
         ditolak mesin
Def 1. Finite State Automata dinyatakan oleh 5 tuple
           M=(Q , Σ , δ , S , F )
              Q = himpunan state
              Σ = himpunan simbol input
              δ = fungsi transisi δ : Q × Î£
              S = state awal / initial state , S ∈ Q
              F = state akhir, F ⊆ Q
Contoh diatas, 
Q = {Genap, Ganjil} 
Σ = {0,1}  
S = Genap 
F = {Ganjil }
δ
0
1
Genap Genap Ganjil
Ganjil Ganjil Genap

atau

δ(Genap,0) = Genap
δ(Genap,1) = Ganjil
δ(Ganjil,0) = Ganjil
δ(Ganjil,1) = Genap
Jenis FSA
Deterministic Finite Automata (DFA) : dari suatu state ada tepat satu state berikutnya untuk setiap simbol masukan yang diterima
Non-deterministic Finite Automata (NFA) : dari suatu state ada 0, 1 atau lebih state berikutnya untuk setiap simbol masukan yang diterima

Deterministic Finite Automata
  • Contoh : pengujian parity ganjil.
  • Contoh lain : Pengujian untuk menerima bit string dengan banyaknya 0 genap,
    serta banyaknya 1 genap.
    ♦ 0011 : diterima.
    ♦ 10010 : ditolak, karena banyaknya 0 ganjil
  • Diagram transisi-nya :
diagram
  • DFA nya
    Q = {q0 , q1 , q2 , q3 }
    Σ = {0,1}
    S = q0
    F = { q0}
    fungsi transisi
δ
0
1
q0 q2 q1
q1 q3 q0
q2 q0 q3
q3 q1 q2
  • Contoh lain DFA : Variabel dalam bahasa pascal diawali oleh huruf (besar/kecil),
    dan diikuti dengan huruf atau angka.
pascal
  • Contoh DFA lainnya :
contoh
By di 2 comments:
Label:

Tuesday, 18 October 2011

Pengenalan Teori Bahasa dan otomata

October 18, 2011 otomata , 2 Comments
Menurut American Heritage Dictionary, otomata berarti :
1. A robot
2. One that behaves in an automatic or mechanical fashion

Sedangkan otomata dalam dunia matematikan berarti :
‘Berkaitan dengan teori mesin abstrak, yaitu mesin sekuensial yang menerima input, dan mengeluarkan output, dalam bentuk diskrit.’
Contoh :
+ Mesin Jaja / Vending machine
+ Kunci kombinasi
+ Parser / compiler
Teori otomata dan bahasa formal, berkaitan dalam hal :
  • Pembangkitan  kalimat/generation : menghasilkan semua kalimat dalam bahasa L (language) berdasarkan aturan yang dimilikinya
  • Pengenalan kalimat / recognition : menentukan suatu string (kalimat) termasuk
    sebagai salah satu anggota himpunan L (language)
Bahasa Formal
Suatu kalimat dibentuk dengan menerapkan serangkaian aturan produksi pada sebuah simbol ‘akar’. Proses penerapan aturan produksi dapat digambarkan sebagai suatu diagram pohon.
TEORI DASAR
Def. 1 Sebuah string dengan panjang n yang dibentuk dari himpunan A adalah barisandari n simbol
         a1a2...an ai ∈ A
Panjang string x dituliskan dengan |x|
Def 2 String kosong (null string), dilambangkan dengan ε adalah untaian dengan panjang 0 dan tidak berisi apapun. Panjang string x dituliskan dengan |x|
Def 3 Dua buah string a = a1a2...am dan b=b1b2...bn dapat disambungkan menjadi string c dengan panjang m+n sebagai berikut c = a1a2...amb1b2...bn
Operasi penyambungan tersebut dapat pula diterapkan pada himpunan
Z=XY = {st | s ∈X ∧ t∈Y}
Def 4 (Closure) . An adalah himpunan string dengan panjang n yang dibentuk dari simbol-simbol di himpunan simbol/alfabet A:
Transitif Closure/Kleen Closure adalah himpunan seluruh string yang dapat dibentuk dari A dengan berbagai panjang
A* = A0 ∪ A1 ∪ A2 ∪ A3 ∪ ...

Jika string kosong dikeluarkan , akan diperoleh positive closure
A+ = A1 ∪ A2 ∪ A3 ∪ ...
Tata Bahasa
Aturan yang disebutkan pada proses pengenalan dan pembangkitan kalimat.
Secara formal, tata bahasa terdiri dari 4 komponen yaitu :
1. Himpunan berhingga, tidak kosong dari simbol-simbol non terminal T1
2. Himpunan berhingga, dari simbol-simbol non-terminal N
3. Simbol awal S ∈ N, yang merupakan salah satu anggota dari himpunan simbol nonterminal.
4. Himpunan berhingga aturan produksi P yang setiap elemennya dituliskan dalam
    bentuk :
                α → β

Dimana α dan β adalah string yang dibentuk dari himpunan T ∪ N dan α harus berisi
paling sedikit satu simbol non-terminal.
Keempat komponen tersebut sering dituliskan sebagai berikut :
         G = (T,N,S,P)
             T : Terminal
             N : Non Terminal
             S : Produksi
             P : Aturan Produksi
Bahasa yang dihasilkan oleh G ditulis sebagai L(G), yaitu himpunan string yang dapat diturunkan dari simbol awal S dengan menerapkan aturan-aturan produksi yang terdapat pada P.
Aturan Produksi
Aturan produksi α→β yang diterapkan pada suatu string w=aαc mengganti kemunculan. α menjadi β, sehingga string tersebut berubah menjadi w=aβc, sehingga dapat dituliskan aαc ⇒ aβc (aαc memproduksi aβc).

Produksi tersebut dapat diterapkan berkali-kali 
        w1 ⇒ w2 ⇒ w3 ⇒ ... ⇒ wn
atau dapat dituliskan 
       w1 ⇒* wn
jika minimal harus ada 1 aturan produksi yang diterapkan : 
       w1 ⇒+ wn

Contoh 1
Tatabahasa G = {{S} , {a,b}, S , P } dengan aturan produksi P adalah
       S → aSb
       S → ε
maka dapat dihasilkan suatu string
       S ⇒ aSb ⇒ aaSbb ⇒aabb
sehingga dapat dituliskan
       S ⇒* aabb

Bahasa yang dihasilkan dari tatabahasa tersebut adalah 
       L(G) = { ε , ab, aabb , aaabbb , aaaabbbb, ... }
atau dapat pula dituliskan
       L(G) = {anbn | n ≥ 0 }

Contoh 2
Tatabahasa G = {{S,A} , {a,b}, S , P } dengan aturan produksi P adalah 
       S → Ab
       A → aAb
       A → ε
maka dapat dihasilkan suatu string
       S ⇒ Ab ⇒b
       S ⇒ Ab ⇒ aAbb ⇒ abb
       S ⇒ Ab ⇒ aAbb ⇒ aaAbbb ⇒ aaAbbb

Bahasa yang dihasilkan dari tatabahasa tersebut adalah 
       L(G) = { b , abb, aabbb , aaabbbb , aaaabbbbb, ... }
atau dapat pula dituliskan
       L(G) = {anbn+1 | n ≥ 0 }</FONT< p>

HIRARKI BAHASA
Kelas
Mesin Pengenal
Reguler Language Finite State Automata
Context Free Language Push Down Automata
Context Sensitive Language Linear Bounded Automata
Unrestricted Language Turing Machine

Kelas
Ruas Kiri
Ruas Kanan
Contoh
Reguler
α ∈ N
 ≤ 1 non terminal
(paling kiri/kanan)		 P → abR
Q → abc
R → Scac
Context Free
α ∈ N
 - (sembarang) P → aQb
Q → abPRS
Context Sensitive
α ∈ (T∪N)+
|α| ≤ |β|
(panjang string α ≤ β)
 aD → Da
AD → aCD
Unrestricted
α ∈ (T∪N)+
 - (sembarang) CB → DB
ADc → ε

NB : Ruas kiri harus memuat paling sedikit 1 buah simbol Non-Terminal (N)
Catatan Kuliah
------------------------------------------------------------------------------------------------
S → aN | aSa
α           β

T = Terminal ( huruf Kecil)--> a
N = Non Terminal ( huruf Besar) --> S,N
Non Terminal dapat menjadi Terminal, tapi tidak sebaliknya.

A* ={ε,a,aa,aaa,…}
A+={a,aa,aaa,…}
A2= {ε,a,aa}
By di 2 comments:
Label: