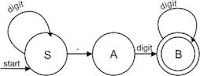
Menurut American Heritage Dictionary, otomata berarti :
1. A robot
2. One that behaves in an automatic or mechanical fashion

Sedangkan otomata dalam dunia matematikan berarti :
‘Berkaitan dengan teori mesin abstrak, yaitu mesin sekuensial yang menerima input, dan mengeluarkan output, dalam bentuk diskrit.’
Contoh :
+ Mesin Jaja / Vending machine
+ Kunci kombinasi
+ Parser / compiler
Teori otomata dan bahasa formal, berkaitan dalam hal :

• Pembangkitan  kalimat/generation : menghasilkan semua kalimat dalam bahasa L (language) berdasarkan aturan yang dimilikinya
• Pengenalan kalimat / recognition : menentukan suatu string (kalimat) termasuk
  sebagai salah satu anggota himpunan L (language)

Bahasa Formal
Suatu kalimat dibentuk dengan menerapkan serangkaian aturan produksi pada sebuah simbol ‘akar’. Proses penerapan aturan produksi dapat digambarkan sebagai suatu diagram pohon.
TEORI DASAR
Def. 1 Sebuah string dengan panjang n yang dibentuk dari himpunan A adalah barisandari n simbol
         a₁a₂...a_n a_i ∈ A
Panjang string x dituliskan dengan |x|
Def 2 String kosong (null string), dilambangkan dengan ε adalah untaian dengan panjang 0 dan tidak berisi apapun. Panjang string x dituliskan dengan |x|
Def 3 Dua buah string a = a₁a₂...a_m dan b=b₁b₂...b_n dapat disambungkan menjadi string c dengan panjang m+n sebagai berikut c = a1a2...amb1b2...bn
Operasi penyambungan tersebut dapat pula diterapkan pada himpunan
Z=XY = {st | s ∈X ∧ t∈Y}
Def 4 (Closure) . Aⁿ adalah himpunan string dengan panjang n yang dibentuk dari simbol-simbol di himpunan simbol/alfabet A:
Transitif Closure/Kleen Closure adalah himpunan seluruh string yang dapat dibentuk dari A dengan berbagai panjang
A* = A⁰ ∪ A¹ ∪ A² ∪ A³ ∪ ...

Jika string kosong dikeluarkan , akan diperoleh positive closure
A⁺ = A¹ ∪ A² ∪ A³ ∪ ...
Tata Bahasa
Aturan yang disebutkan pada proses pengenalan dan pembangkitan kalimat.
Secara formal, tata bahasa terdiri dari 4 komponen yaitu :
1. Himpunan berhingga, tidak kosong dari simbol-simbol non terminal T1
2. Himpunan berhingga, dari simbol-simbol non-terminal N
3. Simbol awal S ∈ N, yang merupakan salah satu anggota dari himpunan simbol nonterminal.
4. Himpunan berhingga aturan produksi P yang setiap elemennya dituliskan dalam
    bentuk :
                α → β

Dimana α dan β adalah string yang dibentuk dari himpunan T ∪ N dan α harus berisi
paling sedikit satu simbol non-terminal.
Keempat komponen tersebut sering dituliskan sebagai berikut :
         G = (T,N,S,P)
             T : Terminal
             N : Non Terminal
             S : Produksi
             P : Aturan Produksi
Bahasa yang dihasilkan oleh G ditulis sebagai L(G), yaitu himpunan string yang dapat diturunkan dari simbol awal S dengan menerapkan aturan-aturan produksi yang terdapat pada P.
Aturan Produksi
Aturan produksi α→β yang diterapkan pada suatu string w=aαc mengganti kemunculan. α menjadi β, sehingga string tersebut berubah menjadi w=aβc, sehingga dapat dituliskan aαc ⇒ aβc (aαc memproduksi aβc).

Produksi tersebut dapat diterapkan berkali-kali 
        w₁ ⇒ w₂ ⇒ w₃ ⇒ ... ⇒ w_n
atau dapat dituliskan 
       w₁ ⇒* w_n
jika minimal harus ada 1 aturan produksi yang diterapkan : 
       w₁ ⇒⁺ w_n

Contoh 1
Tatabahasa G = {{S} , {a,b}, S , P } dengan aturan produksi P adalah
       S → aSb
       S → ε
maka dapat dihasilkan suatu string
       S ⇒ aSb ⇒ aaSbb ⇒aabb
sehingga dapat dituliskan
       S ⇒* aabb

Bahasa yang dihasilkan dari tatabahasa tersebut adalah 
       L(G) = { ε , ab, aabb , aaabbb , aaaabbbb, ... }
atau dapat pula dituliskan
       L(G) = {aⁿbⁿ | n ≥ 0 }

Contoh 2
Tatabahasa G = {{S,A} , {a,b}, S , P } dengan aturan produksi P adalah 
       S → Ab
       A → aAb
       A → ε
maka dapat dihasilkan suatu string
       S ⇒ Ab ⇒b
       S ⇒ Ab ⇒ aAbb ⇒ abb
       S ⇒ Ab ⇒ aAbb ⇒ aaAbbb ⇒ aaAbbb

Bahasa yang dihasilkan dari tatabahasa tersebut adalah 
       L(G) = { b , abb, aabbb , aaabbbb , aaaabbbbb, ... }
atau dapat pula dituliskan
       L(G) = {anbⁿ⁺¹ | n ≥ 0 }</FONT< p>

HIRARKI BAHASA

Kelas	Mesin Pengenal
Reguler Language	Finite State Automata
Context Free Language	Push Down Automata
Context Sensitive Language	Linear Bounded Automata
Unrestricted Language	Turing Machine

Kelas	Ruas Kiri	Ruas Kanan	Contoh
Reguler	α ∈ N	≤ 1 non terminal (paling kiri/kanan)	P → abR Q → abc R → Scac
Context Free	α ∈ N	- (sembarang)	P → aQb Q → abPRS
Context Sensitive	α ∈ (T∪N)+	|α| ≤ |β| (panjang string α ≤ β)	aD → Da AD → aCD
Unrestricted	α ∈ (T∪N)+	- (sembarang)	CB → DB ADc → ε

NB : Ruas kiri harus memuat paling sedikit 1 buah simbol Non-Terminal (N)
Catatan Kuliah
------------------------------------------------------------------------------------------------
S → aN | aSa
α           β

T = Terminal ( huruf Kecil)--> a
N = Non Terminal ( huruf Besar) --> S,N
Non Terminal dapat menjadi Terminal, tapi tidak sebaliknya.

A* ={ε,a,aa,aaa,…}
A⁺={a,aa,aaa,…}
A²= {ε,a,aa}