GoJo pepPo

Friday, 11 November 2011

Finite State Automata (fsa)

Unknown November 11, 2011 otomata , 2 Comments

Model matematika yang dapat menerima input dan mengeluarkan output
Memiliki state yang berhingga banyaknya dan dapat berpindah dari satu state ke state lainnya berdasar input dan fungsi transisi
Tidak memiliki tempat penyimpanan/memory, hanya bisa mengingat state terkini.
Mekanisme kerja dapat diaplikasikan pada : elevator, text editor, analisa leksikal, pencek parity.

Contoh pencek parity ganjil :

Misal input : 1101
         Genap 1 Ganjil 1 Genap 0 Genap 1 Ganjil
         diterima mesin
Misal input : 1100
         Genap 1 Ganjil 1 Genap 0 Genap 0 Genap
         ditolak mesin
Def 1. Finite State Automata dinyatakan oleh 5 tuple
           M=(Q , Σ , δ , S , F )
              Q = himpunan state
              Σ = himpunan simbol input
              δ = fungsi transisi δ : Q × Σ
              S = state awal / initial state , S ∈ Q
              F = state akhir, F ⊆ Q
Contoh diatas,
Q = {Genap, Ganjil}
Σ = {0,1}
S = Genap
F = {Ganjil }

δ	0	1
Genap	Genap	Ganjil
Ganjil	Ganjil	Genap

atau

δ(Genap,0) = Genap
δ(Genap,1) = Ganjil
δ(Ganjil,0) = Ganjil
δ(Ganjil,1) = Genap
Jenis FSA
Deterministic Finite Automata (DFA) : dari suatu state ada tepat satu state berikutnya untuk setiap simbol masukan yang diterima
Non-deterministic Finite Automata (NFA) : dari suatu state ada 0, 1 atau lebih state berikutnya untuk setiap simbol masukan yang diterima

Deterministic Finite Automata

Contoh : pengujian parity ganjil.
Contoh lain : Pengujian untuk menerima bit string dengan banyaknya 0 genap,
serta banyaknya 1 genap.
♦ 0011 : diterima.
♦ 10010 : ditolak, karena banyaknya 0 ganjil
Diagram transisi-nya :

DFA nya
Q = {q0 , q1 , q2 , q3 }
Σ = {0,1}
S = q0
F = { q0}
fungsi transisi

δ	0	1
q₀	q₂	q₁
q₁	q₃	q₀
q₂	q₀	q₃
q₃	q₁	q₂

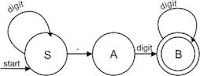
Contoh lain DFA : Variabel dalam bahasa pascal diawali oleh huruf (besar/kecil),
dan diikuti dengan huruf atau angka.

Contoh DFA lainnya :

Tuesday, 18 October 2011

Pengenalan Teori Bahasa dan otomata

Unknown October 18, 2011 otomata , 2 Comments

Menurut American Heritage Dictionary, otomata berarti :
1. A robot
2. One that behaves in an automatic or mechanical fashion

Sedangkan otomata dalam dunia matematikan berarti :
‘Berkaitan dengan teori mesin abstrak, yaitu mesin sekuensial yang menerima input, dan mengeluarkan output, dalam bentuk diskrit.’
Contoh :
+ Mesin Jaja / Vending machine
+ Kunci kombinasi
+ Parser / compiler
Teori otomata dan bahasa formal, berkaitan dalam hal :

Pembangkitan kalimat/generation : menghasilkan semua kalimat dalam bahasa L (language) berdasarkan aturan yang dimilikinya
Pengenalan kalimat / recognition : menentukan suatu string (kalimat) termasuk
sebagai salah satu anggota himpunan L (language)

Bahasa Formal
Suatu kalimat dibentuk dengan menerapkan serangkaian aturan produksi pada sebuah simbol ‘akar’. Proses penerapan aturan produksi dapat digambarkan sebagai suatu diagram pohon.
TEORI DASAR
Def. 1 Sebuah string dengan panjang n yang dibentuk dari himpunan A adalah barisandari n simbol
         a₁a₂...a_n a_i ∈ A
Panjang string x dituliskan dengan |x|
Def 2 String kosong (null string), dilambangkan dengan ε adalah untaian dengan panjang 0 dan tidak berisi apapun. Panjang string x dituliskan dengan |x|
Def 3 Dua buah string a = a₁a₂...a_m dan b=b₁b₂...b_n dapat disambungkan menjadi string c dengan panjang m+n sebagai berikut c = a1a2...amb1b2...bn
Operasi penyambungan tersebut dapat pula diterapkan pada himpunan
Z=XY = {st | s ∈X ∧ t∈Y}
Def 4 (Closure) . Aⁿ adalah himpunan string dengan panjang n yang dibentuk dari simbol-simbol di himpunan simbol/alfabet A:
Transitif Closure/Kleen Closure adalah himpunan seluruh string yang dapat dibentuk dari A dengan berbagai panjang
A* = A⁰ ∪ A¹ ∪ A² ∪ A³ ∪ ...

Jika string kosong dikeluarkan , akan diperoleh positive closure
A⁺ = A¹ ∪ A² ∪ A³ ∪ ...
Tata Bahasa
Aturan yang disebutkan pada proses pengenalan dan pembangkitan kalimat.
Secara formal, tata bahasa terdiri dari 4 komponen yaitu :
1. Himpunan berhingga, tidak kosong dari simbol-simbol non terminal T1
2. Himpunan berhingga, dari simbol-simbol non-terminal N
3. Simbol awal S ∈ N, yang merupakan salah satu anggota dari himpunan simbol nonterminal.
4. Himpunan berhingga aturan produksi P yang setiap elemennya dituliskan dalam
    bentuk :
                α → β

Dimana α dan β adalah string yang dibentuk dari himpunan T ∪ N dan α harus berisi
paling sedikit satu simbol non-terminal.
Keempat komponen tersebut sering dituliskan sebagai berikut :
         G = (T,N,S,P)
             T : Terminal
             N : Non Terminal
             S : Produksi
             P : Aturan Produksi
Bahasa yang dihasilkan oleh G ditulis sebagai L(G), yaitu himpunan string yang dapat diturunkan dari simbol awal S dengan menerapkan aturan-aturan produksi yang terdapat pada P.
Aturan Produksi
Aturan produksi α→β yang diterapkan pada suatu string w=aαc mengganti kemunculan. α menjadi β, sehingga string tersebut berubah menjadi w=aβc, sehingga dapat dituliskan aαc ⇒ aβc (aαc memproduksi aβc).

Produksi tersebut dapat diterapkan berkali-kali
        w₁ ⇒ w₂ ⇒ w₃ ⇒ ... ⇒ w_n
atau dapat dituliskan
       w₁ ⇒* w_n
jika minimal harus ada 1 aturan produksi yang diterapkan :
       w₁ ⇒⁺ w_n

Contoh 1
Tatabahasa G = {{S} , {a,b}, S , P } dengan aturan produksi P adalah
       S → aSb
       S → ε
maka dapat dihasilkan suatu string
       S ⇒ aSb ⇒ aaSbb ⇒aabb
sehingga dapat dituliskan
       S ⇒* aabb

Bahasa yang dihasilkan dari tatabahasa tersebut adalah
       L(G) = { ε , ab, aabb , aaabbb , aaaabbbb, ... }
atau dapat pula dituliskan
       L(G) = {aⁿbⁿ | n ≥ 0 }

Contoh 2
Tatabahasa G = {{S,A} , {a,b}, S , P } dengan aturan produksi P adalah
       S → Ab
       A → aAb
       A → ε
maka dapat dihasilkan suatu string
       S ⇒ Ab ⇒b
       S ⇒ Ab ⇒ aAbb ⇒ abb
       S ⇒ Ab ⇒ aAbb ⇒ aaAbbb ⇒ aaAbbb

Bahasa yang dihasilkan dari tatabahasa tersebut adalah
       L(G) = { b , abb, aabbb , aaabbbb , aaaabbbbb, ... }
atau dapat pula dituliskan
       L(G) = {anbⁿ⁺¹ | n ≥ 0 }</FONT< p>

HIRARKI BAHASA

Kelas	Mesin Pengenal
Reguler Language	Finite State Automata
Context Free Language	Push Down Automata
Context Sensitive Language	Linear Bounded Automata
Unrestricted Language	Turing Machine

Kelas	Ruas Kiri	Ruas Kanan	Contoh
Reguler	α ∈ N	≤ 1 non terminal (paling kiri/kanan)	P → abR Q → abc R → Scac
Context Free	α ∈ N	- (sembarang)	P → aQb Q → abPRS
Context Sensitive	α ∈ (T∪N)+	\|α\| ≤ \|β\| (panjang string α ≤ β)	aD → Da AD → aCD
Unrestricted	α ∈ (T∪N)+	- (sembarang)	CB → DB ADc → ε

NB : Ruas kiri harus memuat paling sedikit 1 buah simbol Non-Terminal (N)
Catatan Kuliah
------------------------------------------------------------------------------------------------
S → aN | aSa
α β

T = Terminal ( huruf Kecil)--> a
N = Non Terminal ( huruf Besar) --> S,N
Non Terminal dapat menjadi Terminal, tapi tidak sebaliknya.

A* ={ε,a,aa,aaa,…}
A⁺={a,aa,aaa,…}
A²= {ε,a,aa}

Wednesday, 1 June 2011

Kode Status HTTP

Unknown June 01, 2011 TipsdanTrik , 0 Comments

Jika anda pada waktu melakukan permintaan ke sebuah alamat HTTP URL dan mendapatkan pesan-pesan error atapun pesan status, disini terdapat beberapa pesan-pesan error maupun status pada HTTP berikut penjelasannya yang biasanya sering anda temui jika melakukan permintaan ke sebuah alamat HTTP URL.

200 OK
Permintaan telah berhasil.
301 Moved Permanently
Dokumen telah dipindahkan ke URL ini.
302 Found
Dokumen telah dipindahkan ke URL ini.
303 See Other
Jawaban untuk permintaan anda berada di URL ini.
304 Not Modified
Salinan cache akan digunakan.
400 Bad Request
Browser mengirim permintaan dan server tidak dapat memahami.
401 Authorization
Membutuhkan autorisasi untuk memasuki URL ini.
403 Forbidden
Anda tidak memiliki izin untuk mengakses server ini.

404 Not Found
Dokumen tidak ada.

405 Method Not Allowed
Metode GET yang diminta tidak diperbolehkan untuk URL

408 Request Time-out
Server timeout.

410 Gone
Proses yang diminta tidak lagi tersedia pada server ini dan tidak ada alamat forwarding.

411 Length Required
Permintaan yang diminta metode GET memerlukan memerlukan Content-length yang valid

412 Precondition Failed
Prasyarat pada permintaan untuk dievaluasi URL bernilai false.

413 Request Entity Too Large
Proses yang diminta tidak memperbolehkan permintaan data dengan menggunakan metode GET atau jumlah data yang diberikan pada permintaan melebihi batas kapasitas.

414 Request-URI Too Large
Panjang URL yang diminta melebihi batas kapasitas untuk server ini

415 Unsupported Media Type
Permintaan data yang diberikan tidak dalam format yang dapat diterima untuk diproses oleh ini.

500 Internal Server Error
Server mengalami kesalahan internal atau misconfiguration dan tidak dapat memenuhi permintaan Anda.

501 Method Not Implemented
Metode GET ke URL tidak didukung

502 Bad Gateway
Server proxy menerima respon tidak valid dari upstream server.

503 Service Temporarily Unavailable
Server untuk sementara tidak dapat melayani permintaan anda karena pemeliharaan downtime atau masalah kapasitas .

506 Variant Also Negotiates
Ini menunjukkan kesalahan konfigurasi.

Membuat shortcut Hibernate

Unknown June 01, 2011 TipsdanTrik , Windows 0 Comments

Hibernate pada Windows merupakan salah satu fitur yang cukup menarik. Dengan mengaktifkan hibernate maka pada saat Anda membuka kembali komputer, Windows tidak akan memulai proses booting lagi dari awal tapi langsung ke posisi di mana semua aplikasi dan dokumen yang terakhir kali Anda buka. Untuk mengaktifkan hibernate bisa dari menu Turn Off Computer pada Start Menu, kemudian tekan dan tahan tombol Shift dan klik pada menu Hibernate. Untuk mempercepat proses hibernate Anda bisa membuat shortcutnya sebagai berikut :

Klik kanan pada Desktop.
Piilh menu New > Shortcut.
Pada bagian Type of location of the item diisi dengan:
%windir%\system32\rundll32.exe PowrProf.dll, SetSuspendState
Klik tombol Next.y
Beri nama pada shortcut tersebut, misalnya Hibernate.
Klik tombol Finish. Maka akan terbentuk satu icon shortcut baru seperti ini :

Sekian dari saya semoga bermanfaat.

Menghentikan proses dari DOS Prompt

Unknown June 01, 2011 TipsdanTrik , Windows 0 Comments

Untuk menghentikan proses (aplikasi dan service) yang sedang berjalan pada Windows saya yakin Anda sering melakukannya dari Windows Task Manager. Selain cara tersebut, ada cara lain yang dapat Anda lakukan yaitu dengan melalui DOS Prompt Caranya adalah sebagai berikut:

Masuk ke dos prompt dengan mengetikkan cmd dari menu Start > Run.
Tulis tasklist dan tekan enter, maka akan tampil daftar proses yang sedang berjalan seperti gambar di bawah ini:

Cari nama proses yang ingin Anda stop, lalu cari nomer PID-nya.
Misalnya Anda ingin menghentikan program Firefox, maka tulis: tskill 2564, lalu tekan enter.
Selesai

Menyembunyikan file dalam gambar

Unknown June 01, 2011 TipsdanTrik , Windows 0 Comments

File merupakan sesuatu yang sangat berharga bagi kita, apalagi file-file yang sangat rahasia. Bila file-file ini bocor atau diketahui oleh orang lain bisa sangat berbahaya. Saya akan berbagi sedikit tips disini bagaimana cara menyimpan file-file rahasia anda tersebut ke dalam sebuah gambar. Kita akan menggunakan dua teknik, yaitu melalui DOS Prompt dan melalui Batch file. Jadi anda dapat menggunakan salah satu dari dua teknik tersebut yang sesuai dengan anda.
Silahkan Ikuti langkah-langkah dibawah ini :

Pastikan komputer anda harus sudah terinstal program untuk mengkompres file, bisa WinRAR, 7-ZIP atau yang lainnya. Windows sendiri sudah punya alat untuk mengkompres data dengan ekstensi .ZIP. Tapi agar lebih efisien anda dapat menggunakan WinRAR, selain dapat mengkompres data hingga batas minimum sehingga file dapat tersembunyi dengan aman tanpa dicugai, WinRAR juga dapat meng-enskripsi file dengan password sehingga data akan jauh lebih aman.
Siapkan file rahasia anda, bisa itu video, document atau lainnya dan sebuah gambar untuk menyembunyikan file tersebut, misalnya disini saya mempunyai sebuah file vidio.3gp yang akan saya sembunyikan dan sebuah file gambar.jpg untuk tempat menyembunyikan file vidio.3gp. Kemudian simpanlah kedua file tersebut dalam satu direktori (folder) yang sama.
Kompres vidio.3gp, disini saya menggunakan WinRAR. Dengan cara klik kanan di vidio.3gp lalu pilih Add to vidio.rar. Maka akan terciptafile baru dengan nama vidio.rar.

Hasilnya :
Setelah semua file telah dikompres, maka kita akan memasuki tahap menggabungkan file. Disini lah anda dapat memilih menggunakan DOS Promtp atau Batch file. Saya akan memulai dengan menggunakan DOS Prompt selanjutnya baru menggunakan Batch file.
Buka Command Prompt dengan cara Klik Start Menu > Run ketik cmd
Kemudian masuk ke direktori tempat nyimpan file-file tadi. Karena saya menyimpannya di E:\, maka ketikkan E: lalu enter.

masukan perintah berikut :
copy /b gambar.jpg+vidio.rar hasil.jpg

copy = perintah untuk menyalin
/b = atribut perintah salin yang berarti menyalin secara Binary
gambar.jpg+vidio.rar = file yang akan disalin, dalam hal ini kita sekaligus menggabungkan 2 file
hasil.jpg = file hasil salin

Gambar diatas menunjukkan bahwa proses telah sukses. Untuk memastikannya bukalah folder tempat anda menyimpan file-file tadi. Jika berhasil, maka akan muncul sebuah file baru bernama hasil.jpg.

Sekarang kita akan mencoba melalui batch file. Sebenarnya sih sama aja caranya, hanya mediumnya saja yang berbeda.
Sekarang bukalah aplikasi notepad dengan cara Start menu > Run > ketik notepad > OK atau start menu > all program > Accessories > Notepad.

Lalu ketik script berikut :
@echo off
copy /b gambar.jpg+vidio.rar hasil.jpg

Simpan script tersebut di derektori yang sama dengan nama hide.bat dan pada Save as type pilih All files kemudian klik Save.
Tutup semua jendela program yang terbuka. Kemudian bukalah folder tempat anda menyimpan file-file tadi. Double klik pada file hide.bat yang telah kita buat tadi. Jika berhasil, maka akan muncul sebuah file baru bernama hasil.jpg.

Cobalah perhatikan file hasil.jpg tersebut. Sekilas tampak tidak akan ada bedanya dengan file gambar.jpg kecuali ukuran filenya yang berubah (besar filenya adalah gabungan dari vidio.rar dengan gambar.jpg).

Anda tetap dapat membuka file tersebut dengan Image Viewer atau ACDsee Quick View. Tidak ada tanda-tanda bahwa ada sebuah rahasia besar didalamnya. Untuk membuka file rahasianya anda cukup dengan klik kanan hasil.jpg > Open With > Choose Program > pilih WinRar > lalu klik OK. File rahasia anda akan muncul dihadapan anda. Anda dapat mengextract file tersebut sebagaimana anda mengextract file rar pada umumnya. File sumber dapat anda hapus jika mau.

Disinilah sebenarnya inti dari persembunyiannya. Coba anda pikirkan, dalam kondisi wajar tidak mungkin ada orang membuka file gambar dengan aplikasi file compressor (WinRAR). Tentunya dapat dipastikan orang akan membuka sebuah file gambar dengan Image Viewer. Dengan memanfaatkan kebiaasaan ini setidaknya file anda akan tersembunyi dengan aman. Kini anda dapat mengirimkan file-file rahasia anda kepada rekan-rekan anda dengan tenang. Tentunya jangan lupa anda memberitahukan rekan anda cara membukanya.

Sunday, 29 May 2011

Daftar Kode Blue Screen Windows XP & Solusinya

Unknown May 29, 2011 TipsdanTrik , Windows 0 Comments

Ketika Windows XP mendeteksi sebuah masalah yang tidak dapat diperbaiki, Windows XP akan menampilkan STOP Message (Pesan STOP). Message ini adalah pesan kerusakan dalam bentuk teks yang memberikan informasi mengenai kondisi yang terjadi.
STOP Message terkadang merujuk kepada BSoD (Blue Screen of Death) yang mengandung informasi spesifik yang dapat membantu Anda mendiagnosa dan memungkinkan Anda memperbaiki masalah yang terdeteksi oleh kernel Windows.

Catatan : daftar ini tidak menyeluruh dan tidak ditujukan untuk menyelesaikan setiap error/kerusakan yang terjadi. Daftar ini hanyalah panduan untuk masing-masing pesan dan kemungkinan penyebab serta solusinya. Dengan memahami dasar dari pesan-pesan error juga akan memudahkan Anda untuk berkomunikasi dengan technical support.

Berikut daftarnya :
1. Stop 0×0000000A or IRQL_NOT_LESS_OR_EQUAL
Pesan Stop 0×0000000A mengindikasikan bahwa proses kernel-mode atau driver mencoba mengakses lokasi di memori namun tidak mempunyai permission (ijin), atau pada kernel IRQL (interrupt request level) yang terlalu tinggi. Proses kernel-mode hanya bisa mengakses proses-proses lain yang mempunyai IRQL kurang dari atau sama dengan miliknya sendiri.

Pesan Stop ini umumnya terjadi karena kesalahan atau tidak kompatibelnya (tidak cocok) hardware dan software. Bisa juga terjadi karena setting BIOS yang kurang tepat.

SOLUSI : Pesan Stop 0×0000000A kemungkinan muncul setelah menginstall driver, system service, ataupun firmware yang salah. Jika pesan Stop memberikan daftar nama driver, disable, hapus, atau roll back (mengembalikan driver ke versi yang bekerja dengan baik) driver yang salah tersebut. Jika men-disable atau menghapus driver menyelesaikan masalah, hubungi manufaktur device (hardware) yang bermasalah untuk kemungkinan update driver yang tersedia. Pesan Stop ini juga mungkin terjadi karena hardware yang rusak atau bermasalah. Jika pesan Stop menunjukkan sebuah kategori device tertentu (video atau disk adapter, contohnya), coba lepas atau ganti hardware tersebut untuk menentukan apakah benar hardware tersebut sumber masalahnya. Jika Anda mengalami pesan Stop ini ketika meng-update Windows XP menjadi sp1, 2, ataupun 3, kemungkinan permasalahan terjadi akibat driver yang tidak kompatibel, system service, scanner virus, atau backup. Untuk mencegah hal ini, sebelum melakukan update Windows, konfigurasi hardware Anda menjadi seminim mungkin fiturnya, dan hapus semua driver third-party (tambahan) dan sistem servis (termasuk antivirus). Setelah update Windows selesai, hubungi manufaktur hardware Anda untuk mendapatkan update yang kompatibel dengan versi service pack (sp) Windows XP Anda.

Jika Anda tidak yakin dengan ketiga pesan di atas, cobalah mereset setting-an BIOS Anda menjadi seperti semula.

2. Stop 0×0000001E or KMODE_EXCEPTION_NOT_HANDLED
Pesan Stop 0×0000001E mengindikasikan bahwa kernel Windows XP mendeteksi sebuah instruksi prosesor ilegal atau yang tidak diketahui. Penyebab pesan Stop ini 0×0000001E mirip dengan penyebab pesan Stop 0×0000000A, yaitu karena pelanggaran akses dan memori yang tidak valid. Biasanya error-handler (pengendali error) default dari Windows XP akan mengatasi masalah ini jika tidak terdapat error-handling routines didalam kode instruksi yang dijalankan.

SOLUSI : Pesan Stop 0×0000001E umumnya terjadi setelah meng-install driver yang rusak atau system service, atau mungkin juga ada masalah pada hardware (seperti memori dan konflik IRQ). Jika pesan Stop memberikan daftar nama driver, disable, hapus, atau roll back (mengembalikan driver ke versi yang bekerja dengan baik) driver yang salah tersebut. Jika men-disable atau menghapus driver menyelesaikan masalah, hubungi manufaktur device (hardware) yang bermasalah untuk kemungkinan update driver yang tersedia. Jika pesan Stop mencantumkan file Win32k.sys, sumber kerusakan kemungkinan adalah program “remote-control” third-party. Jika program sejenis itu terinstall, Anda mungkin bisa me-disable-nya melalui safe mode. Jika tidak, gunakan Recovery Console untuk secara manual menghapus file system service yang menyebabkan masalahnya. Permasalahan juga dapat disebabkan karena firmware yang tidak kompatibel. Kebanyakan masalah ACPI (Advanced Configuration and Power Interface) dapat diperbaiki dengan mengupdate firmware dengan yang terbaru. Kemungkinan lain karena ruang disk yang tidak mencukupi ketika menginstall aplikasi atau menjalankan fungsi tertentu yang membutuhkan memori lebih. Anda bisa menghapus file-file yang tidak dibutuhkan untuk mendapatkan ruang disk. Gunakan Disk Cleanup untuk menambah ruang disk. Melalui Recovery Console, hapus file temporari (file dengan ekstensi .tmp), file-file cache Internet, file backup aplikasi, dan file .tmp yang dihasilkan oleh Chkdsk.exe atau Autochk.exe. Anda juga bisa memilih untuk menginstall aplikasi di harddisk yang lain yang memiliki ruang lebih atau bisa juga memindahkan data dari harddisk yang penuh ke harddisk yang memiliki ruang lebih. Pesan Stop ini juga mungkin disebabkan oleh kebocoran memori (memory leak) dari aplikasi atau servis yang tidak me-release memori dengan benar. Poolmon (Poolmon.exe) membantu Anda mengisolasi komponen yang menyebabkan kebocoran memori kernel. Untuk informasi lebih lanjut mengenai penanganan kebocoran memori lihat Microsoft Knowledgebase artikel Q177415 (http://support.microsoft.com/kb/177415) : “How to Use Poolmon to Troubleshoot Kernel Memory Leaks” dan Q298102 (http://support.microsoft.com/kb/298102) : “Finding Pool Tags Used by Third Party Files Without Using the Debugger”.

3. Stop 0×00000024 atau 0X00000023 or NTFS_FILE_SYSTEM atau FAT_FILE_SYSTEM
Pesan Stop 0×00000024 menunjukkan bahwa ada masalah didalam Ntfs.sys (file driver yang memungkinkan sistem untuk membaca dan menulis ke NTFS file system drives). Pesan Stop yang mirip, 0×00000023, menunjukkan ada masalah pada sistem file FAT16 atau FAT32 (File Allocation Table).

SOLUSI : SCSI yang malfungsi dan hardware ATA (Advanced Technology Attachment) atau driver dapat juga mempengaruhi kemampuan sistem untuk membaca dan menulis ke dalam disk dan menyebabkan error. Jika menggunakan harddisk SCSI, cek kabel dan masalah perhentian (termination problem) antara kontroler SCSI dan disk. Cek secara berkala Event Viewer untuk pesan error yang berhubungan dengan SCSI atau FASTFAT di dalam System Log atau Autochk di Application Log (Klik kanan pada My Computer, pilih Manage, pada bagian Computer Management – System Tools pilih Event Viewer). Cek tool yang biasa Anda gunakan untuk memonitor sistem Anda secara terus menerus (seperti antivirus, program backup, atau program disk defragmenter) apakah sudah kompatibel dengan Windows XP Anda. Beberapa disk atau adapter ada yang dipaketkan dengan software diagnosa yang bisa Anda gunakan untuk melakukan test hardware.

Cara untuk melakukan test harddisk atau integritas volume :
Metode 1:
1. Buka command prompt (Start – Run – ketikkan cmd)
2. Jalankan tool Chkdsk, yang akan mendeteksi dan mencoba untuk me-resolve struktur sistem file yang corrupt, dengan mengetikkan pada command prompt : chkdsk drive: /f

Metode 2:
1. Klik ganda My Computer dan pilih harddisk yang ingin dicek.
2. Pada menu File, pilih Properties.
3. Pilih tab Tools.
4. Pada bagian box Error-checking, klik Check Now.
5. Pada Check disk options, centang Scan for and attempt recovery of bad sectors. Opsi Automatically fix file system errors dapat juga dicentang.

Jika volume yang Anda pilih sedang digunakan, sebuah pesan akan muncul dan menanyakan apakah akan menunda disk error checking sampai Anda me-restart komputer. Setelah restart, disk error checking akan berjalan dan volume yang sedang dicek tidak akan dapat digunakan selama proses berlangsung. Jika Anda tidak bisa me-restart komputer karena error, gunakan safe mode atau Recovery Console.

Jika Anda tidak menggunakan sistem file NTFS, dan partisi sistem diformat dengan sistem file FAT16 ataupun FAT32 (File Allocation Table), informasi LFN (Long File Name) dapat hilang jika tool harddisk dijalankan melalui command prompt MS-DOS. Command prompt yang muncul ketika menggunakan startup floppy disk atau ketika menggunakan pilihan command prompt dalam sistem multiple boot yang menggunakan partisi FAT16 atau FAT32 dengan

Microsoft Windows 95 OEM Service Release 2 (OSR2), Microsoft Windows 98, atau Microsoft Windows Millenium Edition (Me) yang terinstall. Jangan gunakan tool sistem operasi lain untuk partisi Windows XP.

Memori nonpaged pool mungkin terkuras yang dapat menyebabkan sistem untuk berhenti. Anda bisa menyelesaikan masalah ini dengan menambah RAM, yang akan meningkatkan kuantitas dari memori nonpaged pool yang tersedia untuk kernel.

4. UNEXPECTED_KERNEL_MODE_TRAP (0X0000007F)
Bila Anda mendapatkan pesan error seperti ini, dapat disebabkan karena:
- Overclock Hardware yang berlebihan
- Komponen komputer yang terlalu panas
- BIOS yang korup
- Memory dan CPU yang cacat

5. DATA_BUS_ERROR
Pesan error ini disebabkan karena adanya kemungkinan bahwa memory atau slot memory di motherboard rusak.

6. PAGE_FAULT_IN_NONPAGED_AREA
Pesan error ini disebabkan karena adanya kerusakan hardware, termasuk memory utama, memory video card, atau memory di processor (L2 Cache)

7. INACCESSIBLE_BOOT_DEVICE
Pesan error ini disebabkan karena adanya kesalahan dalam konfigurasi jumper harddisk yang salah, virus boot sector, driver IDE controller yang salah, atau kesalahan driver chipset.

8. VIDEO_DRIVER_INIT_FAILURE
Pesan error ini disebabkan karena adanya Kesalahan terjadi pada instalasi driver video card yang kurang sempurna, restart pada saat instalasi atau juga dapat terjadi karena kesalahan dalam instalasi driver.

9. BAD_POOL_CALLER
Pesan error ini disebabkan karena adanya Kesalahan ini dapat terjadi karena kesalahan atau driver yang tidak kompatibel. Sering terjadi saat melakukan instalasi XP dari upgrade, atau bukan dari instalasi baru.

10. PEN_LIST_CORRUPT
Pesan error ini disebabkan karena adanya kerusakan RAM.

11. MACHINE_CHECK_EXCEPTION
Pesan error ini disebabkan oleh cacatnya CPU, atau yang di overclock secara agresif, serta power supply yang kekurangan daya atau rusak.

Sekian dari ane, mohon maaf atas segala kekurangan, jika ada yang salah atau kurang bisa hubungi ane di gojo.wkc@gmail.com, atau di shoutbox blog ane atau pada halaman Kontak. Terima kasih...

TERIMA KASIH

GoJo pepPo
www.gojopeppo.web.id

Tulisan ini bisa kalian download disini.
Penting!!!
Untuk Download tunggu hingga ada tulisan SKIP AD atau LEWATI kemudian klik Tulisan tersebut!!

Mempercepat Windows dengan Setting Registry

Unknown May 29, 2011 TipsdanTrik , Windows 0 Comments

Registry merupakan kumpulan dari data windows yang dipakai untuk mengatur jalannya sistem operasi windows. Untuk melakukan perubahan pada windows menggunakan program regedit. Caranya RUN lalu ketik regedit. Akan terlihat 6 root keys yang mempunyai tugas yang berbeda setiap key (mungkin tidak perlu dijelaskan satu persatu biar gak bosen bacanya, setuju?). Klo gak dijelasin gak belajar namanya he...he...

1. HKEY_CLASSES_ROOT (subkey dari KEY_LOCAL_MACHINE\Software\Classes)

.::Tempat menyimpan informasi yang akan memastikan bahwa files yang kamu buka dibuka dengan aplikasi yang benar.

2. HKEY_CURRENT_USER (Subkey dari HKEY_USERS)

.::Mengandung beragam informasi tentang user (pengguna yang sedang menggunakan Pc). Bukan cuma profil aja, tapi semua settingan kompy masing-masing user ada disini.

3. HKEY_LOCAL_MACHINE

.::Mengandung informasi tentang setting windows secara keseluruhan bagi seluruh pengguna PC. Setting yang dimaksud disini meliputi hardware dan software.

4. HKEY_USERS

.::Udah jelas khan dari namanya... Yup, isi dari handle key yang satu ini adalah data dari seluruh pengguna PC.

5. HKEY_CURRENT_CONFIG

.::Berisi info tentang profil hardware yang digunakan PC saat komputer nyala.

6. HKEY_DYN_DATA

.::untuk mengetahui tingkat kinerja suatu sistem dan dalam jaringan.

Apa saja yang tidak boleh dilakukan??

.::Jangan menggunakan kode registry dari versi windows yang berbeda

.::Jangan pernah meninggalkan Registry Editor dalam keadaan terbuka.

.::Jangan pernah menyalin registry dari komputer lain kecuali kamu faham benar dengan apa yang kamu lakukan.

.::Jangan coba-coba menghapus Handle Key

Berikut ini adalah trik-trik simple untuk mempercepat windows yang saya kumpulkan dari berbagai sumber di google ( lupa sumbernya :) ). Efektifitas trik-trik ini mungkin berbeda-beda, tips-tips berikut mungkin bisa membuat komputer anda tidak stabil. Maka jangan lupa lakukan backup registry sebelum tweaking.

1. Cara Back up registry

Start>Run>regedit>File>Export kasih nama backup.reg anda klik ok done

Agar lebih aman lagi jika terjadi kesalahan maka disarankan untuk membackup semua data-data penting.

2. Mendisable Service Windows yg tidak diperlukan.

Karena windows ditujukan untuk berbagai user dan tugas, maka windows membuat service yang sebenarnya tidak terlalu diperlukan. Service-service berikut ini seringkali memakan resouce yang tidak sedikit, dengan mendisable (me-non-aktif-kan) maka komputer kita bisa mendapatkan sedikit boost karenanya. Cara mendisable service:

a. Klik Start>Run>ketik “services.msc”

b. Dobel klik service yg hendak diubah

c. Ubah startup type menjadi ‘Disable”

Berikut ini service-service yang biasanya tidak digunakan (terutama untuk PC yang tidak terhubung jaringan). Alerter (berguna untuk mengirim pesan perhatian –alert– pada sistem jaringan; kalau untuk PC stand alone nggak perlu, bisa di – disable).

Clipbook (lebih sering nggak digunakan, matikan saja)

Computer browser (untuk browsing computer dalam jaringan; kalau nggak terhubung jaringan, matikan saja)

Distributed Link Tracking Client Error reporting service (menampilkan pesan error — lebih sering nggak perlu, dapat dimatikan)

Fast User Switching Help and Support (Jika anda mengunakan windows help, maka langkah ini diskip aja)

Human Interface Access Devices Indexing service (mengindeks file supaya pencarian menjadi cepat, namun dapat malah memperlambat kinerja, matikan saja).

IPSEC service (mengatur policy keamanan IP – kalau komputer stand alone nggak perlu diatur, dapat dimatikan)

Messenger (untuk memunculkan window messenger bila terkoneksi internet. kalau nggak matikan saja) Netmeeting Remote Desktop sharing (untuk netmeeting. Nggak perlu untuk yang hanya sering “copy darat”. Matikan)

Portable Media Serial Number Remote Desktop Help Session Manager Remote Procedure Call Locator Remote Registry (untuk mengedit registri komputer lain dalam satu jaringan. Nggak perlu. bisa dimatikan)

Remote Registry Service Secondary Logon Routing & Remote Access (Pokoknya yang remote2 utu semuanya berhubungan dengan jaringan. kalau nggak perlu bisa dimatikan)

Security Center (yang nampilkan setting firewall di SP2. Matikan)

Server System event notifikation (untuk memberitahu event yang terjadi di komputer. lebih sering nggak perlu. bisa dimatikan)

Task Scheduler (untuk menjadwalkan tindakan otomatis, misalkan scan, koneksi internet dll. sering nggak perlu. Matikan)

TCP/IP NetBIOS Helper Telnet (berguna untuk berhubungan dengan jaringan. untuk komputer yang hanya terhubung dengan power supply doang, jelas ini perlu dimatikan)

Upload Manager Universal Plug and Play Device Host Windows Time (untuk sinkronisasi waktu dengan GMT yang memerlukan koneksi internet. sangat nggak perlu. matikan.)

Window Firewall/internet connection (kalau koneksi internet lebih sering dari wartel, lebih baik dimatikan saja)

Wireless Zero Configuration (Jangan didisable jika anda mengunakan Wireless)

Workstation

Itu adalah beberapa service yang dapat dimatikan. Untuk yang lainnya, kegunaan bisa dibaca sendiri di bagian description. Kalau misalkan salah satu program nggak bisa jalan gara-gara butuh service tersebut, aktifkan lagi service-nya. Dengan cara diatas, komputer anda insya Allah akan berjalan lebih cepat.

3. Meningkatkan kecepatan internet

a. Klik Start>Run>ketik “gpedit.msc”

b. Lihat dan perhatikan “group policy editor” lanjut

c. ke “Local Computer Policy” > “Computer Configuration” > “Administrative Templates” > “Network” > “QOS Packet Scheduler” > “Limit Reservable Bandwidth”

d. setelah itu akan keluar tab “Limit Reservable bandwidth”

e. Anda lihat sendiri kan posisi choice-nya masih dalam keadaan “Not Configured“,

f. pilih “enabled”

g. dan lihat Bandwidth Limit (%) “20“, sekarang gantilah menjadi “0”

h. sekarang klik “OK”

i. dan tutup semua “windows” yang terbuka dan restart-lah komputer Anda.

Note : Hanya untuk windows xp pro.

4. Matikan System restore

System restore bisa bermanfaat jika komputer bermasalah, akan tetapi semua restore point yg disimpan bisa memakan ruangan yg cukup besar di harddisk. System restore membebani karena selalu memonitor sistem, dengan mendisable system restore maka sebagian resorce bisa dialokasikan untuk hal yg lain.

a. Buka Control Panel

b. Klik Performance and Maintenance

c. Klik System

d. Klik System Restore tab

e. Klik ‘Turn off System Restore on All Drives’

f. Klik ‘Ok’

5. Defrag Pagefile

Menjaga susunan pagefile anda sehingga membuat kinerja semakin meningkat. Salah satu cara tebaik untuk melakukan ini adalah dengan menciptakan sebuah partisi yang terpisah pada hard drive anda hanya untuk pagefile anda, sehingga tidak bisa dipengaruhi oleh penggunaan disk normal. Cara lain untuk menjaga susunan pagefile anda adalah dengan menjalankan PageDefrag. Aplikasi ini sedikit mudah dapat digunakan untuk menyusun pagefile anda, dan juga dapat diatur untuk menyusun pada setiap pagefile di PC anda.

Untuk menginstal:

a. Download dan Jalankan PageDefrag,
b. kasih centang pada "Defrag at next Reboot",
c. Klik OK
d. Reboot

6. Mempercepat akses Folder

Dengan mendisable Last Access Update. Jika anda memiliki banyak folder dan subdirectories, maka akses ke Direktory-direktory Windows XP terasa sangat berat dan seringkali cuman membuang waktu. Dengan mengupdate time stamp di registry, yaitu last access update untuk semua sub directory.

a. Start>Run>regedit

b. “HKEY_LOCAL_MACHINE\System\CurrentControlSet\Contr ol\FileSystem”

c. Klik kanan di bagian yang kanan (cari area yg kosong), lalu pilih ‘DWORD Value’

d. Bikin DWORD Value dengan nama ‘NtfsDisableLastAccessUpdate’

e. Klik kanan pada value baru terus pilih ‘Modify’

f. Ubah data menjadi ’1′

g. Klik ‘OK’

7. Me-non-aktifkan Microsoft System Sounds

Secara default MS sound systems membuat komputer berbunyi/bersuara ketika booting awal, shutdown, error, dll. Skenario suara windows jelas-jelas membuat komputer lebih lambat (terutama dalam waktu shutdown dan booting awal), untuk me-non-aktifkan silahkan ikuti langkah berikut:

1. Buka Control Panel

2. Klik Sounds and Audio Devices

3. Klik tab Sounds

4. Pilih “No Sounds” dari Sound Scheme

5. Klik “No”

6. Klik “Apply”

7. Klik “OK”

8. Mempercepat waktu Boot

Untuk mempercepat botting windows langkah pertama klik Start>Run ketikkan msconfig – Ok. Pada system configuration utility pilih tab dialog pilih startup hilangkan centang yang tidak perlu di load pertama kali Fitur yg lumayan asik dari Windows XP adalah kemampuan untuk mendefrag ketika ada dalam proses booting. Boot Defrag pada prinsip menata file-file yang relevan dengan booting secara berurutan. Secara default fitur ini telah diaktifkan pada beberapa Build Windows, tapi beberapa build windows tidak, ada baiknya kalo kita cross check terhadap fitur yg satu ini.

a. Start Menu>Run

b. Ketik Regedit

c. HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Dfrg\BootOpt imizeFunction

d. Cari “Enable” dibagian kanan regedit

e. Klik “Modify”

f. Pilih “Y to enable”

g. Reboot Tambahan: Bootvis juga bisa dicoba, untuk memangkas waktu boot dengan manufer yg manis. Untuk menghilangkan screen boot windows langkah pertama klik Start>Run ketikkan msconfig – Ok pada system configuration utility pilih tab dialog pilih boot.ini kemudian berilah tanda centang pada .NOGUIBOOT

9. Mempercepat Performa Swapfile

Jika anda memiliki ram lebih besar dari 256MB bisa dibilang tweaking yg ini akan membuat sistem anda berjalan lebih cepat. Tweaking ini pada dasarnya PC kita mengunakan setiap byte dari memori fisik yg terpasang di komputer kita, SEBELUM mengunakan swap file.

a. Start>Run

b. “msconfig.exe”>ok

c. Klik tab System.ini

d. Klik tanda plus pada tab 386enh

e. Klik kotak new kemudian ketik “ConservativeSwapfileUsage=1″

f. Klik OK

g. Restart

10. Mempercepat Loading Windows Menu

Tweak ini adalah tweaking fav saya, karena akan komputer kita terasa lebih cepat. Tweaking ini membuang waktu delay ketika kita mengklik menu dan windows XP menampakkan Menu.

a. Start>Run

b. Regedit>Ok

c. “HKEY_CURRENT_USER\Control Panel\Desktop\”

d. Pilih/Sorot “MenuShowDelay”

e. Klik kanan dan pilih “Modify’

f. Ketik angka “0″

11. Mempercepat Loading Program

Tweaking ini bisa berjalan untuk sebagian besar program. Jika program tidak mau loading seperti yang diharapkan, silahkan aja dikembalikan ke setting semula.

a. Klik kanan pada icon/shortcut yg berkaitan dengan program.

b. Properties

c. Pada kotak ‘target’, tambahkan ‘ /prefetch:1′ diakhir kalimat.

d. Klik “Ok” gampang kan, Program akan loading lebih cepat.

12. Mempercepat Shutdown Windows XP

Tweaking ini mengurangi waktu tunggu secara otomatis ketika windows sudah menerima instruksi untuk shutdown.

a. Start>Run ketik ‘Regedit’>OK

b. ‘HKEY_CURRENT_USER\Control Panel\Desktop\’

c. Sorot ‘WaitToKillAppTimeout’

d. Klik kanan dan pilih modify

e. Ubah value menjadi ’1000′

f. Klik ‘OK’

g. Sorot ‘HungAppTimeout’

h. Klik kanan dan pilih modify

i. Ubah value menjadi ’1000′

j. Klik ‘OK’

k. ‘HKEY_USERS\.DEFAULT\Control Panel\Desktop’ sorot WaitToKillAppTimeout’

l. Klik kanan dan pilih modify

m. Ubah value ke ’1000′

n. Klik ‘OK’

o. ‘HKEY_LOCAL_MACHINE\System\CurrentControlSet\Contr ol\’

p. sorot ‘WaitToKillServiceTimeout’

q. Klik kanan dan pilih modify

r. Ubah value menjadi ’1000′

s. Klik ‘OK’

13. Menghilangkan Prefetch

Ini adalah file log history windows,biasanya memperlambat kinerja windows

a. Start>Run “regedit”;

b. cari [HKEY_LOCAL_MACHINE\SYSTEM\ CurrentControlSet\Control\ Session Manager\ Memory Management\ PrefetchParameters\ EnablePrefetcher];

c. ubah nilainya menjadi 0 (disable)

d. reboot computer

e. Atau

f. Untuk menghapusnya secara berkala bisa melalui cara seperti di bawah ini:

g. Buka Windows Explorer

h. Pada Address Bar ketik : C:\Windows\Prefetch

i. Maka anda akan menenmukan banyak file dengan extensi .PF

j. Block semua file tersebut atau ctrl+a

k. Delete

l. Restart komputer

14. Menghilangkan Recent Document

a. Start>Run “gpedit.msc”

b. klik Administrative Templates di bawah User Configuration

c. klik Start Menu and taksbar

d. klik Do not keep history of recenly opened documents

e. pilih enabled

15. Membersihkan Recent Document

a. Start>Run “gpedit.msc”

b. klik Administrative Templates di bawah User Configuration

c. klik Start Menu and taksbar

d. klik Clear history of recenly opened documents on exit

e. pilih enabled

16. Memodifikasi “Send To” pada klik kanan

a. Explorer -> C:\Documents and Settings -> klik folder Administrator (atau sesuai dengan username kamu)

b. Tools -> Folder Option -> View -> Show hidden File and Folder (untuk menampilkan file yang tersembunyi)

c. Klik folder ‘Send To’

d. modifikasi (hapus atau buat shortcut baru) yang mau kamu tampilkan pada klik kanan ‘Send To’, bila kamu menghapus semua shortcut maka yang ditampilkan pada klik kanan ‘Send To’ hanyalah removable device semisal flashdisk

17. Mengembalikan ‘Show hidden File and Folder’

Jika hilang atau terkena virus, copy paste script di bawah pada Notepad lalu simpan dengan ekstensi .reg , misal hidden.reg lalu double klik file hidden.reg

[HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\ Explorer\Advanced\Folder\Hidden] “Text”=”@shell32.dll,-30499″ “Type”=”group” “Bitmap”=hex(2):25,00,53,00,79,00,73,00,74,00,65,00,6d,00,52,00,6f,00,6f,00,74,\ 00,25,00,5c,00,73,00,79,00,73,00,74,00,65,00,6d,00,33,00,32,00,5c,00,53,00,\ 48,00,45,00,4c,00,4c,00,33,00,32,00,2e,00,64,00,6c,00,6c,00,2c,00,34,00,00,\ 00 “HelpID”=”shell.hlp#51131″ [HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\ Explorer\Advanced\Folder\Hidden\NOHIDDEN] “RegPath”=”Software\\Microsoft\\Windows\\CurrentVersion\\Explorer\\Advanced” “Text”=”@shell32.dll,-30501″ “Type”=”radio” “CheckedValue”=dword:00000002 “ValueName”=”Hidden” “DefaultValue”=dword:00000002 “HKeyRoot”=dword:80000001 “HelpID”=”shell.hlp#51104″ [HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\ Explorer\Advanced\Folder\Hidden\SHOWALL] “RegPath”=”Software\\Microsoft\\Windows\\CurrentVersion\\Explorer\\Advanced” “Text”=”@shell32.dll,-30500″ “Type”=”radio” “CheckedValue”=dword:00000001 “ValueName”=”Hidden” “DefaultValue”=dword:00000002 “HKeyRoot”=dword:80000001 “HelpID”=”shell.hlp#51105″

18. Membuat Shorcut tanpa nama

a. klik kanan shortcut

b. rename

c. tahan Alt+255 (ini adalah kode Ascii untuk ‘Space’, kalo tidak salah)

19. Menghilangkan Recycle Bin dari dekstop icon

a. Start>Run “gpedit.msc”

b. klik Administrative Templates di bawah User Configuration

c. klik Dekstop

d. klik Remove Recycle Bin Icon from dekstop

e. pilih enabled

20. Memperbaiki Registry Windows

a. Start>Run “cmd”

b. ketik “scanreg/restore”

c. enter

21. Menghilangkan Run Dari start menu

a. Start>Run “gpedit.msc”

b. klik Administrative Templates di bawah User Configuration

c. klik Start Menu and taksbar

d. klik Remove Run from Start menu

e. pilih enabled

22. Membuat background image pada drive atau flashdisk

a. Start dari explorer pilih “Tools”

b. pilih ‘Show hidden file’ dan uncheck ‘hide protected operating system file’

c. OK

d. misal, klik pada drive D: buat file dekstop.ini

e. isi dengan beberapa baris di bawah ini :

[.ShellClassInfo] [{BE098140-A513-11D0-A3A4-00C04FD706EC}] Attributes=1 IconArea_Image=image.jpg IconArea_Text=0×0000FF

f. save

g. kembalikan ’show hidden file’ & ‘hide protected OS file’ ke kondisi semula (opsional)

h. untuk flashdisk, copy paste file dekstop.ini beserta image yang ingin ditampilkan ke flasdisk kamu

Ket :

IconArea_Image=image.jpg -> mengarah pada nama file image kamu (nama harus sama,gunakan path jika image berbeda folder)

IconArea_Text=0×0000FF -> mengarah pada warna tulisan untuk foldermu (format blue-green-red) jadi,jika warna merah yang seharusnya RGB FF0000 menjadi BGR 0000FF,jika ingin warna hitam maka ganti dengan 0×000000

24. Login Otomatis

a. HKEY_LOCAL_MACHINE/SOFTWARE/Microsoft/WindowsNT/CurrentVersion/Winlogon

b. Klik ganda AltDefaultUserName dan masukkan username account yang dipilih.

c. Klik ganda AutoAdminLogon dan masukkan angka 1 pada Value Data.

d. Buat sebuah DWORD Value baru dan beri nama DefaultPassword.

e. Klik ganda DefaultPassword dan masukkan password account yang dipilih pada Value Data.

25. Mencegah perubahan Menu Start

a. HKEY_CURRENT_USER/Software/Microsoft/Windows/CurrentVersion/Policies/Explorer

b. Buat sebuah DWORD Value baru dan beri nama NoChangeStartMenu.

c. Klik ganda NoChangeStartMenu dan masukkan angka 1 pada Value Data.

26. Membersihkan semua icon pada Desktop

a. HKEY_CURRENT_USER/Software/Microsoft/Windows/CurrentVersion/Policies/Explorer

b. Buat sebuah DWORD Value baru dan beri nama NoDesktop.

c. Klik ganda pada NoDesktop dan masukkan angka 1 pada Value Data

27. Membuat Desktop lebih Stabil

a. HKEY_CURRENT_USER/Software/Microsoft/Windows/CurrentVersion/Explorer

b. Buat sebuah DWORD Value baru dan beri nama DesktopProcess.

c. Klik ganda DesktopProcess dan masukkan angka 1 pada Value Data

28. Menyembunyikan System Tray

a. HKEY_LOCAL_MACHINE\Software\Microsoft\Windows\Curr entVersion\Policies\Explorer

b. Jika key Explorer belum ada buatlah sebuah DWORD Value baru dan beri nama NoTrayItemsDisplay.

c. Klik ganda NoTrayItemsDisplay dan masukkan angka 1 pada Value Data.

d. Untuk mengembalikan System Tray masukkan angka 0 pada Value Data.

29. Menonaktifkan Klik Kanan Pada Desktop

a. HKEY_CURRENT_USER/Software/Microsoft/Windows/CurrentVersion/Policies/Explorer

b. Buat sebuah DWORD Value baru dan beri nama NoViewContextMenu.

c. Klik ganda pada NoViewContextMenu dan masukkan angka 1 pada Value Data.

30. Menonaktifkan menu properties My Computer

a. HKEY_CURRENT_USER/Software/Microsoft/Windows/CurrentVersion/Policies/Explorer

b. Buat sebuah DWORD Value baru dan beri nama NoPropertiesMyComputer.

c. Klik ganda NoPropertiesMyComputer dan masukkan angka 1 pada Value Data.

d. HKEY_LOCAL_MACHINE/Software/Microsoft/Windows/CurrentVersion/Policies/Explorer

e. Buat sebuah DWORD Value baru dan beri nama NoPropertiesMyComputer.

f. Klik ganda NoPropertiesMyComputer dan masukkan angka 1 pada Value Data.

g. Jika key Explorer tidak ada, buat yang baru dengan mengklik menu Edit > New > Key dan beri nama Explorer.

31. DVD di Windows Media Player

a. HKEY_CURRENT_USER/Software/Microsoft/MediaPlayer/Player/Settings

b. Pilih menu Edit > New > String Value dan beri nama DVDUI.

c. Klik ganda DVDUI dan masukkan teks Yes pada Value Data

32. Menambah identitas Windows Media Player

a. HKEY_CURRENT_USER/Software/Policies/Microsoft

b. HKEY_LOCAL_MACHINE/SOFTWARE/Policies/Microsoft/Windows

c. Klik Edit > New > Key dan beri nama WindowsMediaPlayer.

d. Klik Edit > New > String Value dan beri nama TitleBar.

e. Klik ganda TitleBar dan masukkan teks yang diinginkan pada Value Data.

33. Mengembalikan akses ke CD-ROM

a. HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Contro l\Class\{4D36E965-E325-11CE-BFC1-08002BE10318}

b. Hapus subkey LowerFilters dan UpperFilters dengan menekan tombol Delete

34. Membersihkan sampah registry

a. HKEY_CLASSES_ROOT/Application

b. HKEY_CURRENT_USER/Software

c. HKEY_LOCAL_MACHINE/SOFTWARE

d. Pilih salah satu subkey yang merupakan nama software yang ingin dihapus, kemudian tekan tombol Del.

35. Membersihkan sampah uninstall

a. HKEY_LOCAL_MACHINE/SOFTWARE/Microsoft/Windows/CurrentVersion/Uninstall

b. Hapus subkey yang memiliki nama yang sama dengan software yang telah di-uninstall

36. Menghapus daftar program yang tak diinginkan dari Add/Remove Program

a. HKEY_LOCAL_MACHINE\ SOFTWARE\ Microsoft\ Windows\ CurrentVersion\ Uninstall

b. Hapus subkey yang berisikan program yang tidak diinginkan dengan menekan tombol Del.

37. Menjalankan program saat StartUp

a. HKEY_LOCAL_MACHINE/SOFTWARE/Microsoft/Windows/CurrentVersion/Run

b. Pilih menu Edit > New > String Value dengan nama Winamp misalnya.

c. Klik ganda pada value tersebut dan masukkan path tempat program tersebut terinstall (C:\ProgramFiles\Winamp\Winamp.exe).

38. Menghapus StartUp Items dari MSCONFIG

a. Klik Start > Run > ketik msconfig, kemudian klik pada tab startup, hilangkan tanda centang pada program yang ingin dihapus dari daftar startup.

b. HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Run

c. HKEY_CURRENT_USER\SOFTWARE\Microsoft\Windows\CurrentVersion\Run

d. Hapus subkey yang berisikan program-program yang tidak diinginkan dengan menekan tombol Del.

39. Mengganti AM – PM dangan Pagi – Sore

a. HKEY_CURRENT/International _USER/Control Panel

b. Klik ganda s1159 dan ubah teks AM dengan PAGI.

c. Klik ganda s2359 dan ubah teks PM dengan SORE.

40. Menonaktifkan fungsi AutoRun

a. HKEY_CURRENT_USER/Software/Microsoft/Windows/CurrentVersion/Policies/Explorer

b. Klik ganda NoDriveTypeAutoRun dan masukkan angka 95 pada Value Data.

41. Mematikan Program Not Responding secara Automatis

a. HKEY_USERS/.DEFAULT/Control Panel/Desktop

b. Klik ganda AutoEndTasks dan masukkan angka 1 pada Value Data.

42. Tweaking memori pada windows Xp

a. HKEY_LOCAL_MACHINE/SYSTEM/CurrentControlSet/Control/SessionManager/MemoryManagement

b. Klik ganda pada DisablePagingExecutive dan masukkan angka 1 pada Value Data.

c. Apabila diaktifkan,Windows tidak akan melakukan paging file ke dalam hard disk. Sistem operasi dan program-program menjadi lebih responsif. Disarankan untuk komputer yang memiliki memori lebih dari 128MB.

d. Klik ganda pada LargeSystemCache dan masukkan angka 1 pada Value Data. Jika diaktifkan, sistem akan mengalokasikan seluruh memori (kecuali 4 MB untuk disk caching) untuk file caching. Komputer akan melakukan caching kernel XP di dalam memory sehingga Windows XP dapat berjalan lebih cepat.

43. Unload .dll untuk mempercepat akses memori

a. HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Explorer

b. Pilih menu Edit > New > Key dan beri nama AlwaysUnloadDLL.

c. Pada option Default Value masukkan angka 1.

44. Menyembunyikan Device Manager

a. HKEY_CURRENT_USER/Software/Microsoft/Windows/CurrentVersion/Policies

b. Pilih menu Edit > New > Key dan beri nama System.

c. Di subkey System buatlah sebuah DWORD Value baru dan beri nama NoDevMgrPage.

d. Klik ganda NoDevMgrPage dan masukkan angka 1 pada Value Data.

45. Mengoptimalkan Harddisk disaat computer dalam keadaan Idle

a. HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\OptimalLayout

b. Buatlah sebuah DWORD Value Baru dan beri nama EnableAutoLayout.

c. Klik ganda EnableAutoLayout dan masukkan angka 1 pada Value Data.

46. Mengosongkan temporary internet file saat exit

a. HKEY_CURRENT_USER\Software\Microsoft\Windows\CurrentVersion\Internet Settings\Cache

b. HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Internet Settings\Cache

c. Buat sebuah DWORD Value baru dan beri nama Persistent.

d. Klik ganda Persistent dan masukkan angka 0 pada Value Data

47. Menyembunyikan drive pada My Komputer

a. HKEY_CURRENT_USER\Software\Microsoft\Windows\CurrentVersion\Policies\Explorer

b. "NoDrives"=dword:data

c. Data= (drive yang akan di hide)

d. Daftar drive :

A: 1, B: 2, C: 4, D: 8, E: 16, F: 32, G: 64, H: 128, I: 256, J: 512, K: 1024, L: 2048, M: 4096, N: 8192, O: 16384, P: 32768, Q: 65536, R: 131072, S: 262144, T: 524288, U: 1048576, V: 2097152, W: 4194304, X: 8388608, Y: 16777216, Z: 33554432, ALL: 67108863

48. Menskip registrasi Windows XP

a. HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\WindowsNT\CurrentVersion

b. "RegDone"="1"

49. Menghiasi toolbar windows explorer dengan gambar

a. HKEY_CURRENT_USER\Software\Microsoft\Internet Explorer\Toolbar

b. "BackBitmapShell"="C:\GAMBARMU.bmp"

:::: Ganti C:\GAMBARMU.bmp dengan lokasi file .bmp yang akan anda pergunakan sebagai background

50. Merubah logo bola bumi pada internet explorer

a. HKEY_CURRENT_USER\Software\Microsoft\Internet Explorer\Toolbar

b. "BrandBitmap"="C:\GAMBARMU.bmp"

c. "SmBrandBitmap"="C:\GAMBARMU.bmp"

::: Usahakan file gambar berformat .bmp dengan ukuran lebar sekitar 2 cm dan tingi sekitar 15 kb dengan resolusi 96 px/inci

51. Mematikan fasilitas display properties

Display settings muncul apabila, klik disembarang desktop pilih properties. Untuk melakukan penguncian cari root keys berikut :

a. HKEY_CURRENT_USER\software\microsoft\win dows\currentversion\policies\ system

b. Buat value baru dengan jenis data DWORD yaitu : NodispCpl